①数と表現
(1)2進数の表現
私たちが日常生活の中で利用している数は、10進数と呼ばれる方式で表現されており、値が10になるときに桁が1つ繰り上がるものです。一方、コンピュータの世界では、値が2になると桁が繰り上がる2進数と呼ばれる方式で数を取り扱い、2進数における1桁ビット(bit)と表現します(4桁の2進数であれば4ビット)。
| 10進数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2進数 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
(2)基数変換
異なる進数間で数値を置き換えることを基数変換と呼びます。2進数と10進数の間における基数変換の方法は以下のとおりです。
例)2進数「1101」から10進数への基数変換
2進数を並べて、2の(n-1)乗の値をかけます(※nは桁数)
1×2^3 | 1×2^2 | 1×2^1 | 1×2^0
求められて足した数字が10進数の値(上記の場合は8+4+0+1で13)
10進数「22」から2進数への基数変換
- 10進数「22」を2で割ります。
- 商とあまりの数を求めます。
- 商が0になるまで繰り返します。
- 求められたあまりの数を最後から順番に並べたものが2進数の値(例の場合は10110)
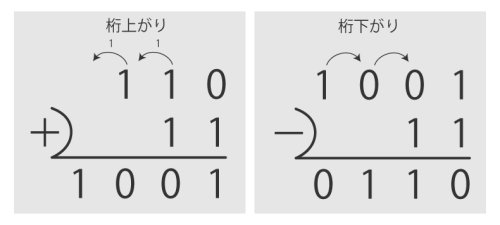
(3)2進数の加算・減算
2進数の加算・減算は10進数と同様に、下の位から計算していきます。
10進数の桁下がりでは、「上の桁から10(10進数)を借りてくる」と表現するのと同じように、2進数の桁下がりも「上の桁から10(2進数)つまり10進数でいうと『2』を借りてくる」と考えると理解しやすいです。
(4)表現可能な数値の範囲
2進数の桁数(ビット数)における表現可能な数値の範囲(パターン)は以下の通りです。
| ビット数 | 参考計算式 | 取り得る値の範囲 |
|---|---|---|
| 4 | 2×2×2×2(2^4) | 0~15(16パターン) |
| 8 | 2^8 | 0~255(256パターン) |
| 12 | 2^12 | 0~4095(4096パターン) |
| 16 | 2^16 | 0~65535(65536パターン) |
②集合
集合とは、明らかな条件によってグループ化されたものの集まりです。集合の条件は命題と呼ばれる表現の組み合わせで表現することができ、命題とは「AまたはB」「AかつB」「Aではない」「Aではなく、かつBである」(例:東京都在住ではなく、25歳以上である)などです。
③論理演算
論理演算とは、複数の条件を式で表し、演算に用いられるようにしたものです。論理演算によって計算される結果は真理値と呼ばれ、取り得る値は限られており、205単元33離散数学以下にそれを示します。
AND演算(論理積)
A=1かつB=1のとき1
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
XOR演算(排他的論理和)
AとBが異なる場合は1
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
OR演算(論理和)
A=1またはB=1のとき1
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
NOT演算(否定)
A=0(A≠1)のとき1
| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
まとめ
今回は離散数学について解説しました。
クレアールではこのほかにもITパスポートに関するコラムを投稿していますので、併せてご覧ください。



